A pdf copy of this article is available here.
Introduction
A study published in March by the COVID-19 Response Team from Imperial College (Ferguson20[1]) appears to have been largely responsible for driving government actions in the UK and, to a fair extent, in the US and some other countries. Until that report came out, the strategy of the UK government, at least, seems to have been to rely on the build up of ‘herd immunity’ to slow the growth of the epidemic and eventually cause it to peter out.
The ‘herd immunity threshold’ (HIT) can be estimated from the basic reproduction rate of the epidemic, R0 – a measure of how many people, on average, each infected individual infects. Standard simple compartmental models of epidemic growth imply that the HIT equals {1 – 1/R0}. Once the HIT is passed, the rate of new infections starts to decline, which should ensure that health systems will not thereafter be overwhelmed and makes it more practicable to take steps to eliminate the disease.
However, the Ferguson20 report estimated that relying on herd immunity would result in 81% of the UK and US populations becoming infected during the epidemic, mainly over a two-month period, based on an R0 estimate of 2.4. These figures imply that the HIT is between 50% and 60%.[2] Their report implied that health systems would be overwhelmed, resulting in far more deaths. It claimed that only draconian government interventions could prevent this occurring. Such interventions were rapidly implemented in the UK, in most states of the US, and in various other countries, via highly disruptive and restrictive enforced ‘lockdowns’.
A notable exception was Sweden, which has continued to pursue a herd immunity-based strategy, relying on relatively modest social distancing policies. The Imperial College team estimated that, after those policies were introduced in mid-March, R0 in Sweden was 2.5, with only a 2.5% probability that it was under 1.5.[3] The rapid spread of COVID-19 in the country in the second half of March suggests that R0 is unlikely to have been significantly under 2.0.[4]
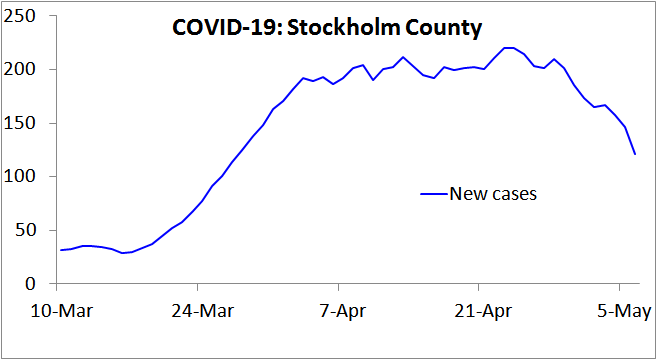
Very sensibly, the Swedish public health authority has surveyed the prevalence of individuals infected by the SARS-COV-2 virus, according to PCR testing, in Stockholm County, the earliest in Sweden hit by COVID-19. They thereby estimated that 17% of the population would have been infected by 11 April, rising to 25% by 1 May 2020.[5] Yet recorded new cases had stopped increasing by 11 April (Figure 1), as had net hospital admissions,[6] and both measures have fallen significantly since. That pattern indicates that the HIT had been reached by 11 April, at which point only 17% of the population appear to have been infected.
How can it be true that the HIT has been reached in Stockholm County with only about 17% of the population having been infected, while an R0 of 2.0 is normally taken to imply a HIT of 50%?
The importance of population inhomogeneity
A recent paper (Gomes et al.[7]) provides the answer. It shows that variation between individuals in their susceptibility to infection and their propensity to infect others can cause the HIT to be much lower than it is in a homogeneous population. Standard simple compartmental epidemic models take no account of such variability. And the model used in the Ferguson20 study, while much more complex, appears only to take into account inhomogeneity arising from a very limited set of factors – notably geographic separation from other individuals and household size – with only a modest resulting impact on the growth of the epidemic.[8] Using a compartmental model modified to take such variability into account, with co-variability between susceptibility and infectivity arguably handled in a more realistic way than by Gomes et al., I confirm their finding that the HIT is indeed reached at a much lower level than when the population is homogeneous. That would explain why the HIT appears to have been passed in Stockholm by mid April. The same seems likely to be the case in other major cities and regions that have been badly affected by COVID-19.
Figure 1. New COVID-19 cases reported in Stockholm County, Sweden, over the 7 days up to the date shown. Note that in Sweden testing for COVID-19 infection was narrowed on 12 March, to focus on people needing hospital care, so from then on only a tiny proportion of infections were recorded as cases. This would account for the lack of growth in cases during the first week plotted. Since hospitalisation usually occurs several days after symptom onset, this change also increases the lag between infection and recording as a case. Accordingly, from mid- March on the 7-day trailing average new cases figure will reflect new infections that on average occurred approximately two weeks earlier.
The epidemiological model used
Like Gomes et al., I use a simple ‘SEIR’ epidemiological model,[9] in which the population is divided into four compartments: Susceptible (uninfected), Exposed (latent: infected but not yet infectious), Infectious (typically when diseased), and Recovered (and thus immune and harmless). This is shown in Figure 2. In reality, the Recovered compartment includes people who instead die, which has the same effect on the model dynamics. The entire population starts in the Susceptible compartment, save for a tiny proportion that are transferred to the Infectious compartment to seed the epidemic. The seed infectious individuals infect Susceptible individuals, who move to the Exposed compartment. Exposed individuals gradually transfer to the Infectious compartment, on average remaining as Exposed for the chosen latent period. Infectious individuals in turn gradually transfer to the Recovered compartment, on average remaining as Infectious for the selected infectious period.
Figure 2. SEIR compartment epidemiological model diagram.
In the case of COVID-19, the diseased (symptomatic) stage is typically reached about 5 days after infection, but an infected individual starts to become infectious about 2 days earlier. I therefore set the average latent period as 3 days.[10]
The infectious period depends mainly on the delay between infectiousness and symptoms appearing and on how quickly an individual reduces contacts with others once they become symptomatic, as well as on how infectious asymptomatic cases are. In an SEIR model, the infective period can be derived by subtracting the latent period from the generation time – the mean interval between the original infection of a person and the infections that they then cause.
The Ferguson20 model assumed a generation time of 6.5 days, slightly lower than a subsequent estimate of 7.5 days.[11] I use 7 days, which is consistent with growth rates near the start of COVID-19 outbreaks.[12] The infectious period is therefore 4 (=7 − 3) days.
I set R0=2.4, the same value Ferguson20 use. On average, while an individual is in the Infectious compartment, the number of Susceptible individuals they infect is R0 × {the proportion of the population that remains in the Susceptible compartment}.
With these settings, the progression of a COVID-19 epidemic projected by a standard SEIR model, in which all individuals have identical characteristics, is as shown in Figure 3. The HIT is reached once 58% of the population has been infected, and ultimately 88% of the population become infected.
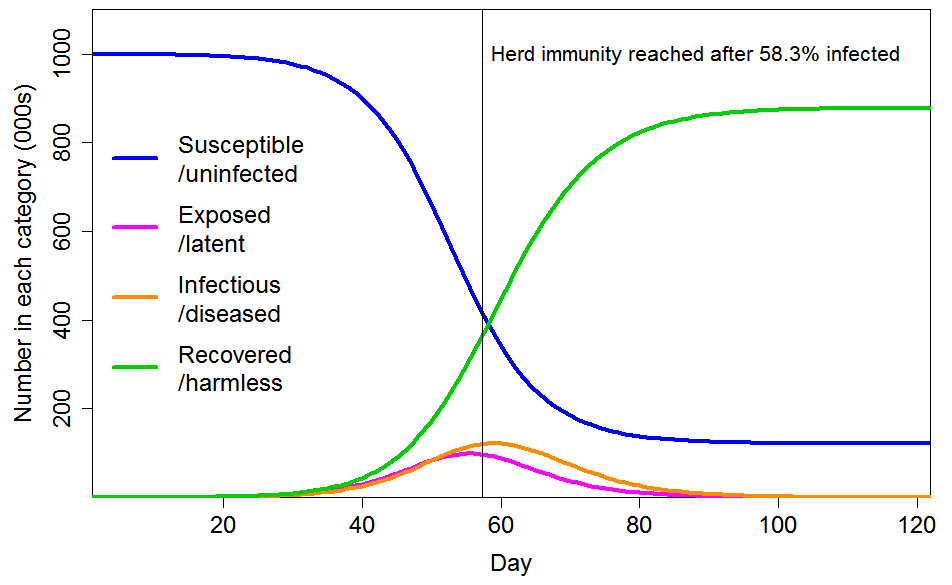
Modifying the basic SEIR model for variability in individual susceptibility and infectivity
The great bulk of COVID-19 transmission is thought to occur directly from symptomatic and pre-symptomatic infected individuals, with little transmission from asymptomatic cases or from the environment.[13] There is strong evidence that a small proportion of individuals account for most infections – the ‘superspreaders’.
A good measure of the dispersion of transmission – the extent to which infection happens through many spreaders or just a few – is the coefficient of variation (CV).[14] Two different estimates of this figure have been published for COVID-19. A Shenzhen-based study[15] estimated that 8.9% of cases were responsible for 80% of total infections, while a multi-country study[16] estimated that 10% were so responsible. In both cases a gamma probability distribution was assumed, as is standard for this purpose. The corresponding CV best estimates and 95% uncertainty ranges are 3.3 (3.0–5.6) and 3.1 (2.2–5.0). These figures are slightly higher than the 2.5 estimated for the 2003 epidemic of SARS.[17]
CV estimates indicate the probability of transmission of an infection. They reflect population inhomogeneity regarding individuals’ differing tendency to infect others, but it is unclear to what extent they also reflect susceptibility differences between individuals. However, since COVID-19 transmission is very largely person-to-person, much of the inhomogeneity in transmission rates will reflect how socially connected individuals are, and how close and prolonged their interactions with other individuals are. As these factors affect the probability of transmission both from and to an individual, as well as causing variation in an individual’s infectivity they should cause the same variation in their susceptibility to infection.
A common social connectivity related factor implies that an individual’s susceptibility and infectivity are positively correlated, and it is not unreasonable to assume a quite strong correlation. However, it seems unrealistic to assume, as Gomes et al. do in one case, that an individual’s infectivity is directly proportional to their personal susceptibility. (In the other case that they model, they assume that an individual’s infectivity is unrelated to their susceptibility.)
Some of the variability in the likelihood of someone infecting a susceptible individual during an interaction will undoubtedly be unrelated to social connectivity, for example the size of their viral load. Likewise, susceptibility will vary with the strength of an individual’s immune system as well as with their social connectivity. I use unit-median lognormal distributions to reflect such social-connectivity unrelated variability in infectivity and susceptibility. Their standard deviations determine the strength of the factor they represent. I model an individual’s overall infectivity as the product of their common social-connectivity related factor and their unrelated infectivity-specific factor, and calculate their overall susceptibility in a corresponding manner.[18]
I consider the cases of CV=1 and CV=2 for the common social connectivity factor that causes inhomogeneity in both susceptibility and infectivity. For unrelated lognormally-distributed inhomogeneity in susceptibility I take standard deviations of either 0.4 or 0.8, corresponding to a CV of 0.417 or 0.947 respectively. Where their gamma-distributed common factor inhomogeneity is set at 1, the resulting total inhomogeneity in susceptibility is respectively 1.17 or 1.65 when the lower or higher unrelated inhomogeneity standard deviations respectively are used; where set at 2 the resulting total inhomogeneity in susceptibility is respectively 2.17 or 2.98. The magnitude of variability in individuals’ social-connectivity unrelated infectivity-specific inhomogeneity factor does not affect the progression of an epidemic or the HIT, so for simplicity I ignore it here.[19]
Results
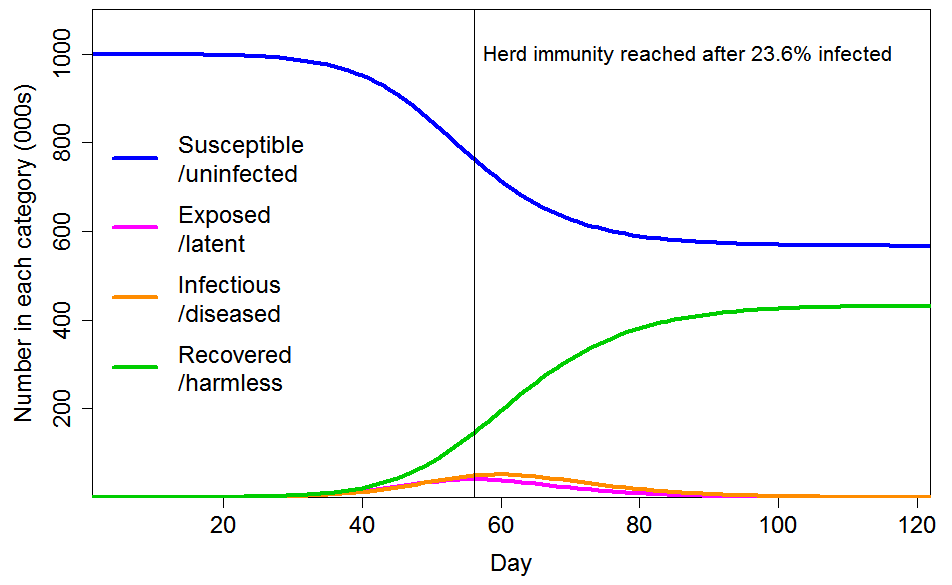
Figure 4 shows the progression of a COVID-19 epidemic in the case of CV=1 for the common social connectivity factor inhomogeneity, with unrelated inhomogeneity in susceptibility having a standard deviation of 0.4. The HIT is 60% lower than for a homogeneous population, at 23.6% rather than 58.3% of the population. And 43% rather than 88% of the population ultimately becomes infected. If the standard deviation of unrelated inhomogeneity in susceptibility is increased to 0.8, the HIT becomes 18.9%, and 35% of the population are ultimately infected.
Figure 4. Epidemic progression in an SEIR model with R0=2.4 and a population with CV=1 common factor inhomogeneity in susceptibility and infectivity and also unrelated multiplicative inhomogeneity in susceptibility with a standard deviation of 0.4.
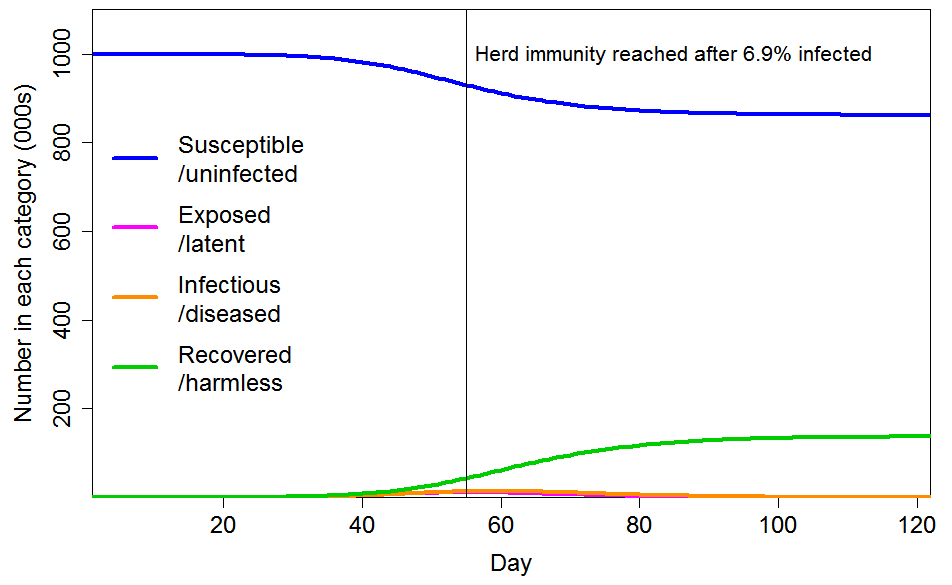
Figure 5 shows the progression of a COVID-19 epidemic in the case of CV=2 for the common social connectivity factor inhomogeneity, with unrelated inhomogeneity in susceptibility having a standard deviation of 0.8. The HIT is only 6.9% of the population, and only 14% of the population ultimately becoming infected. If the standard deviation of unrelated inhomogeneity in susceptibility is reduced to 0.4, those figures become respectively 8.6% and 17%.
Figure 5. Epidemic progression in an SEIR model with R0=2.4 and a population with CV=2 common factor inhomogeneity in susceptibility and infectivity and also unrelated multiplicative inhomogeneity in susceptibility with a standard deviation of 0.8.
Conclusions
Incorporating, in a reasonable manner, inhomogeneity in susceptibility and infectivity in a standard SEIR epidemiological model, rather than assuming a homogeneous population, causes a very major reduction in the herd immunity threshold, and also in the ultimate infection level if the epidemic thereafter follows an unconstrained path. Therefore, the number of fatalities involved in achieving herd immunity is much lower than it would otherwise be.
In my view, the true herd immunity threshold probably lies somewhere between the 7% and 24% implied by the cases illustrated in Figures 4 and 5. If it were around 17%, which evidence from Stockholm County suggests the resulting fatalities from infections prior to the HIT being reached should be a very low proportion of the population. The Stockholm infection fatality rate appears to be approximately 0.4%,[20] considerably lower than per the Verity et al.[21] estimates used in Ferguson20, with a fatality rate of under 0.1% from infections until the HIT was reached. The fatality rate to reach the HIT in less densely populated areas should be lower, because R0 is positively related to population density.[22] Accordingly, total fatalities should be well under 0.1% of the population by the time herd immunity is achieved. Although there would be subsequent further fatalities, as the epidemic shrinks it should be increasingly practicable to hasten its end by using testing and contact tracing to prevent infections spreading, and thus substantially reduce the number of further fatalities below those projected by the SEIR model in a totally unmitigated scenario.
Nicholas Lewis 10 May 2020
Update 11 May: R code used to produce the results and figures in this article is available here
Update 12 May: the reference to “prevalence of antibodies to the SARS-COV-2 virus in Stockholm County” has been corrected; it was in fact the prevalence of SARS-CoV-2 PCR-positive (infectious) individuals that was measured. This citation error has no bearing on any of the arguments made or results presented in this article.
[1] Neil M Ferguson et al., Impact of non-pharmaceutical interventions (NPIs) to reduce COVID-19 mortality and healthcare demand. Imperial College COVID-19 Response Team Report 9, 16 March 2020, https://spiral.imperial.ac.uk:8443/handle/10044/1/77482
[2] A final infection rate of 81% implies, in the context of a simple compartmental model with a fixed, homogeneous population, that the ‘effective R0‘ is between 2.0 and 2.1, and that the HIT is slightly over 50%. Ferguson20 use a more complex model, so it is not surprising that the implied effective R0 differs slightly from the basic 2.4 value that Ferguson20 state they assume.
[3] Flaxman, S. et al., Estimating the number of infections and the impact of non-pharmaceutical interventions on COVID-19 in 11 European countries. Imperial College COVID-19 Response Team Report 13, 30 March 2020, https://www.imperial.ac.uk/mrc-global-infectious-disease-analysis/covid-19/report-13-europe-npi-impact/
[4] Based on the Ferguson20 estimate of a mean generation time of 6.5 days, which appears to be in line with existing evidence, an R0 of 2.0 would result in a daily growth rate of 2.0^(1/6.5)= 11%. That is slightly lower than the peak growth rate in cases in late March in Stockholm County, and in early April in the two regions with the next highest number of cases, in both of which the epidemic took off slightly later than in Stockholm, and in line with the growth rate in Swedish COVID-19 deaths in early April
[5] https://www.folkhalsomyndigheten.se/contentassets/2da059f90b90458d8454a04955d1697f/skattning-peakdag-antal-infekterade-covid-19-utbrottet-stockholms-lan-februari-april-2020.pdf
[6] John Burn-Murdoch, Financial Times Research, 2 May 2020. http://web.archive.org/web/20200507075628/https:/twitter.com/jburnmurdoch/status/1256712090028576768
[7] Gomes, M. G. M., et al. Individual variation in susceptibility or exposure to SARS-CoV-2 lowers the herd immunity threshold. medRxiv 2 May 2020. https://www.medrxiv.org/content/10.1101/2020.04.27.20081893v1
[8] The 81% proportion of the population that Ferguson20 estimated would eventually become infected is only slightly lower than the 88% level implied by their R0 estimate of 2.4 in the case of a homogeneous population.
[9] https://en.wikipedia.org/wiki/Compartmental_models_in_epidemiology#The_SEIR_model
[10] Gomes et al. instead set the latent period slightly longer, to 4 days and treated it as a partly infectious period, unlike in the standard SEIR model.
[11] Li Q, Guan X, Wu P, et al.: Early Transmission Dynamics in Wuhan, China, of Novel Coronavirus-Infected Pneumonia. N Engl J Med. 2020; 382(13):1199–1207.https://www.nejm.org/doi/10.1056/NEJMoa2001316
[12] Once a SEIR model has passed its start up phase, and while a negligible proportion susceptible individuals have been infected, the epidemic daily growth factor is R0^(1/generation time), or 1.10–1.13 for R0=2.0–2.4 if the generation time is 7 days.
[13] L. Ferretti et al., Science 10.1126/science.abb6936 (2020).
[14] The coefficient of variation is the ratio of the standard deviation to the mean of its probability distribution. It is usual to assume a gamma distribution for infectivity, the shape parameter of which equals 1/CV2.
[15] Bi, Qifang, et al. “Epidemiology and transmission of COVID-19 in 391 cases and 1286 of their close contacts in Shenzhen, China: a retrospective cohort study.” The Lancet Infectious Diseases 27 April 2020. https://doi.org/10.1016/S1473-3099(20)30287-5
[16] Endo, Akira, et al. “Estimating the overdispersion in COVID-19 transmission using outbreak sizes outside China.” Wellcome Open Research 5.67 (2020): 67. https://wellcomeopenresearch.org/articles/5-67
[17] Lloyd-Smith, J O et al. “Superspreading and the effect of individual variation on disease emergence.” Nature 438.7066 (2005): 355-359. https://www.nature.com/articles/nature04153
[18] For computational efficiency, I divide the population into 10,000 equal sized segments with their common social connectivity factor increasing according to its assumed probability distribution, and allocate each population segment values for unrelated variability in susceptibility and infectivity randomly, according to their respective probability distributions.
[19] A highly susceptible but averagely infectious person is more likely to be removed from the susceptible pool early in an epidemic, reducing the average susceptibility of the pool. However, no such selective removal occurs for a highly infectious person of averagely susceptibility. Therefore, as Gomes et al. point out, variability in susceptibility lowers the HIT, but variability in infectivity does not do so except to the extent that it is correlated with variability in susceptibility.
[20] On 8 May 2020 reported total COVID-19 deaths in Stockholm County were 1,660, which is 0.40% of the estimated 413,000 of its population who had been infected by 11 April 2020. COVID-19 deaths reported for Stockholm County after 8 May that relate to infections by 11 April 2020 are likely to be approximately balanced by deaths reported by 8 May 2020 that related to post 11 April 2020 infections.
[21] Verity R, Okell LC, Dorigatti I, et al. Estimates of the severity of COVID-19 disease. medRxiv 13 March 2020; https://www.medrxiv.org/content/10.1101/2020.03.09.20033357v1.
[22] Similarly, the HIT may be significantly higher in areas that are very densely populated, have much less inhomogenous populations and/or are repeatedly reseeded from other areas. That would account for the high prevalence of COVID-19 infection that has been found in, for instance, some prisons and residential institutions or in city districts.
Hi Nic,
Very interesting paper.
One comment and one request.
I saw on “the other site” you answering questions about variation in densely populated areas, NYC etc. You might be interested in the (preliminary?) Babbitt-Garland-Johnson preprint on a first step at modelling this: https://arxiv.org/abs/2005.01167
(They aren’t thinking super-spreaders/care homes etc, but its a start.)
Request: can you make your code and model public – eg on github, so that interested people can play with them? Maybe its already there – in which case apologies – but I didn’t find it.
Hi Charles
Thanks for the link. I’ll have a look at the preprint you refer to.
I will make the R code I used, which in effect specifies the SEIR model equations involved, public shortly. I’ll probably make it available on my webpages, as I’m not currently a github user. Either way, I’ll add a link to it at the bottom of this post.
Hi. This is very interesting. I made a similar analysis a few days ago, with roughly the same findings:
https://jsmp.dk/posts/2020-05-07-herdimmunity/
Would you share you code? (Or even more details of the model.) I would like to contrast and compare.
Hi, I have now uploaded working R code that can reproduce the results both in my article and, with suitable settings, those shown in Fig. 3 of the Gomes et al paper. It is not particularly elegant code, but it works.The link is posted on this webpage, in an update at the end of the main text of my article.
Let me know if you have any problems with it.
Sir, I would like to point out that you citation of the Swedish public health authority survey, citation [5] is incorrect. Obviously, you have not read it, which might be due to tha fact that it is written in swedish with no english summary. Nevertheless, you are responsible for your citations. The estimation is NOT based on a survey of antibody prevalence but on the prevalence of SARS-CoV-2 PCR positive patients. From this data the SEIR model is used to estimate the number of cases that would have been infected etc. Thus, the estimate is an extrapolation of rather scarce data, ie % SARS-CoV-2 PCR positives in a random sample of 707 persons performed between March 27 and April 1.
Current antibody studies indicate a much lower prevalence, between 7.5 – 11 % in studies performed during the second half of April.
Many thanks for pointing out this stupid mistake, Mr Gustafsson. I have corrected the relevant wording. I am glad to say that nothing else in the article is affected.
You say that current antibody studies indicate a much lower prevalence of 7.5 – 11%. Please can you confirm whether this relates to the whole of Sweden or just Stockholm County, and also whether these figure are adjusted for test false positive and false negative rates. I would also appreciate a link to where details of these results are given, so that if I cite them I do so accurately. I have so far only been able to find a secondary sources for such results, which stated that “at least 11% of the participants have antibodies to COVID-19”.
Hi Nic
Something I don’t quite understand. You show 3 charts for different values of CV (0, 1, 2) but with the same R0. However, the curves for infections – which I think would be the data used in the course of an epidemic to measure R0 – seem to have very different slopes and hence different R0s: the higher CV, the lower the implied R0.
Wouldn’t that mean that in the cases of heterogeneous populations R0 wouldn’t be estimated at 2.4 (as was the case for C-19 in Wuhan) but something lower, perhaps much lower for the CV=2 chart?
I think the way out of this might be that in Wuhan R0 was estimated in the very early stages of the outbreak. Perhaps for small infection percentages the charts for the 3 different CVs look very similar, before later diverging,
Simon Anthony
Also, am I right to think that Ferguson20 used a CV value of 0.25 to characterise their gamma distribution? If so, I can’t see any justification of this choice in their paper. It seems very low in light of the results of the studies you reference. Of course, in defence of Ferguson et al, the estimates for CV weren’t available until after their paper was published.
Hi Nic
A couple of earlier comments/questions which I made/asked have gone missing but undaunted…
Ferguson20 has the statement: “Individual infectiousness is assumed to be variable, described by a gamma distribution with mean 1 and shape parameter 0.25”, which would imply a CV of 2 for the infectiousness distribution.
Is this at least partially equivalent to the CV = 2 case which you consider? If so, the differences between your results and those of Ferguson20 are presumably due to the spatial distributions and interactions which are included in the latter.
Nic, please ignore the first two of my comments – based on very partial understanding. But I think the third one still stands.
Hi Simon,
I agree that Ferguson20’s statement implies that used CV=2 for their infectivity distribution.
However, although variability in susceptibility lowers the HIT, variability in infectivity does not do so except to the extent that it is correlated with variability in susceptibility. See my note 19. It does not seem that the Ferguson20 model, unlike mine and Gomes et al.’s, had variability in infectivity correlated with variability in susceptibility. So their assumption it is not at all similar to the CV=2 case that i consider.
Very interesting and I think your last two simulations look very similarly to what is actually happening in Sweden. I’m interested in timelines, what was the population density used in your estimation? And how would 24 people/km^2 impact the timelines ?
thanks in advance
w stankiewicz
I didn’t directly use any population density value. But my suggestion of a 17% possible herd immunity threshold related specifically to Stockholm county, which has a population of ~2.4 million people and an area of ~6520 km^2, so about 370 people/km^2.
I would expect the HIT to be considerably lower for 24 people/km^2, as the average number of contacts per day will be lower (and hence R_0 will be lower), but I wouldn’t like to say how much lower the HIT would be.
Hi Nic, I think this is a really valuable contribution to the discussion of why in viral transmission has begun to decline significantly before any population approached the anticipated HIT. One thing that is absent from this model that I think could bring even more clarity and accuracy is a representation of the non-uniformity of R0 related to the seasonality of the virus. Would it be possible to make R0 variable over the course of the model run to represent the inherent change in transmissivity of the virus related to relative humidity and temperature? Some basic details regarding how these variables impact coronaviruses has been recently published here: https://www.medrxiv.org/content/10.1101/2020.05.15.20103416v1
Hi Adam
Thanks!
In principle one could make R0 vary with time to reflect seasonality, but it would add further complication.
Your link doesn’t work for me – can you check it?
Thanks for the response. Not sure why it’s not working. I’ll try again. https://www.medrxiv.org/content/10.1101/2020.05.15.20103416v1
If all else fails, the title is “The Seasonal End of Human Coronavirus Hospital Admissions with Implications for SARS-CoV-2”
Thanks – the link worked fine this time.
Although it does indeed appear that your choice not to model the latents and infectious by more than one “box” doesn’t much affect the resultant herd-immunity threshold, I’ll just mention for what it’s worth that your choice does seem to result in a lower initial growth rate and thus a lower peak in the number of infectious. By my calculations using higher number of “boxes” can make the peak as much as 40% higher. A slight increase in the cumulative number who have been sick would also result.
Since the subject is the herd-immunity threshold, that effect probably is not important in this discussion. I mention it just in case any inferences I’m unaware of are being drawn from early growth rates.
Can you give a link to a source that shows the effect of using multiple boxes (I assume you mean in series, not in parallel) on the initial growth rate? I agree that the point, even if correct, is unlikely to be relevant here.
Sorry, no link; I did the simulation myself.
Specifically, out of a cohort of people who simultaneously become infectious at time t=0, the proportion who remain infectious according to the one-box model decays as 1-pgamma(t, shape = 1, rate = 1/tau.I): an exponential decay. If the infectious component is instead modeled as n boxes, the decay is 1-pgamma(t, shape = n, rate = n/tau.I). If the number of boxes is infinite, the response is 1, ttau.I.
So I used that rectangular-response model (with one-hour time steps) to simulate an infinite number of boxes for both E and I. The peak turned out to be about 40% higher. But, again, the herd-immunity threshold was basically unchanged.
It appears that my last comment got garbled. What it should have said is that the response for an infinite number of boxes is unity before tau.I and zero after tau.I.
Thanks, I understand your point. I agree that a single exponential decay may not be the most realistic way of modelling the progression from I to R, or from E to I. But an infinite number of boxes, which as you say corresponds to a deterministic, fixed infectious or exposed period, may be even more unrealistic. Modelling each of these transitions as a two stage process, so with two E boxes and two I boxes, may be better than the standard single box for each treatment. That is what Thomas House does: https://personalpages.manchester.ac.uk/staff/thomas.house/blog/modelling-herd-immunity.html. However, that would increase the computational burden, which although minor with a single box for each stage is non-negligible with 10,000 boxes at each stage, representing different segments of the population, as I use.
In any event, as you have found, the timing related model structure and parameters, while affecting the speed at which the epidemic progresses, have a negligible effect on non-dimensional results like the HIT, given a fixed (non-dimensional) R_0 and the distributions of common and separate susceptibility and infectivity.
I agree, of course, that the infinite-boxes model is certain to be wrong. But it’s nonetheless useful, as they say, in that it gives us a likely limit on how great the effect of adding boxes can be..
As I said, with an infinite number of boxes the peak in the number of simultaneously infectious seems to be about 40% for the case of N = 1e6, R0=2.4, tau_E = 3 days, and tau_I = 4 days. So at least in that case the peak-value increase won’t much exceed 40% no matter how many boxes you use.
I note, though, that most of that 40% increase would probably result even from adding only a few boxes. At least that’s what is suggested by the resultant change in the eigenvalue, i.e., in the early-days coefficient of exponential-growth. For the above-mentioned parameters, the eigenvalue resulting from only a single E box and a single I box is 0.157/day. By comparison, the eigenvalue for an infinite number of boxes, i.e., for the model that results in a 40% higher peak, is 0.179/day. But dividing the E and I components into only four boxes results in an eigenvalue of 0.174/day, i.e., almost as high as the infinite-boxes model’s. So I’m guessing the peak-value increase would be similarly significant.
Again, though, the effect I’m talking about here is peak infections, not the herd-immunity threshold, which was the subject of your piece; that quantity seems largely unaffected.
Thanks for pursuing this point. It makes sense that using a relatively small number of boxes will get most of the way to the step function response from an infinite number of boxes.
I believe that the probability distribution resulting from dividing the latent and infectious periods into a number of Poisson process boxes, each with the same exponential distribution rate parameter, has a closed form; it has an Erlang distribution, which is a special case of the Gamma distribution.
Researcher Stephen Baum estimated, from data collected in Wuhan, that the mean incubation period (which is longer than the latent period, since infectiousness starts about 2 days prior to symptoms) was 5.5 days, with a median of 5.1 days and a 2.5% – 97.5% CI of 2.2 to 11.5 days. This can be well modelled by an Erlang distribution with shape parameter 5 and rate parameter 5/5.5, corresponding to splitting the 5.5 day mean latent period between 5 boxes. The resulting median latent time is 5.14 days, and the 2.5% – 97.5% CI is 1.8 to 11.3 days; the mean is of course 5.5 days. (With 4 boxes the median is almost as close at 5.05 but the 2.5%-97.5% CI is a bit wide at 1.5-12.1; the 5%-95% CI is 1.9-10.7.)
So, it looks like your 4 box example is close to the best number to choose, although for computational reasons fewer boxes might be used. In fact one could use a single box with the probability of transition set by the Erlang/Gamma PDF, but it would be necessary to keep track of when each individual entered the box, which is likely to negate any advantage from doing so.
Actually, “keeping track of when each individual entered the box” is really what I mostly do. Specifically, I store as time sequences the quantities that correspond to your dSL and dLI, and I convolve them respectively with negatives of the derivatives of the E and I systems’ impulse responses to get equivalents to your dLI and dIR.
This imposes a speed and scalability penalty, not only because of the convolution but also because it requires finer time resolution than Runge-Kutta (or whatever ode() uses) lets you get away with. (I use a one-hour time step.) But it affords me more flexibility in response specification. Consequently, I can get the results of any number of boxes by merely providing the associated impulse response, and I don’t need to provide a separate state variable for each box.
For what it’s worth, I’ll try to provide a relevant excerpt from my script below, although my guess is that the blog-site software will chew it up and make it unintelligible. The “dh.E” and “dh.I” are negatives of the respective impulse responses’ derivatives.
# To make the early-days reproduction number’s effective value equal
# the argument value, we divide by mean(Iy * Sy)–which is unity if Iy and
# Sy are uncorrelated–to arrive at a “force of infection” lambda:
lambda = R0[i – 1] * dt / tau.I / mean(Iy * Sy) * sum(Iy * I[i – 1,])
# Use that to calculate the number of susceptibles who become latents, i.e.,
# join the E component:
delta.SL[i,] = lambda * Sy * S[i – 1,] / N
delta.SL[i, which(delta.SL[i,] > S[i – 1,])] = S[i – 1, which(delta.SL[i,] > S[i – 1,])]
# To find the E-I system’s impulse response we can short-circuit the feedback:
if(shorted) delta.SL[i,] = rep(0, n.bins)
# To calculate the number of exposed who become infectious, we convolve past
# exposed-component additions with the derivative of the exposed component’s
# impulse response:
delta.LI[i,] = colSums(matrix(dh.E[1:min(i – 1, n.E)] *
delta.SL[i – 1:min(i – 1, n.E),], ncol = n.bins))
# To calculate the number of infectious who recover or die, we onvolve past
# infectious-component additions with the derivative of the infectious
# component’s impulse response:
delta.IR[i,] = colSums(matrix(dh.I[1:min(i – 1, n.I)] *
delta.LI[i – 1:min(i, n.I),], ncol = n.bins))
# Use the calculated differences to update the system state:
S[i,] = S[i – 1,] – delta.SL[i,]
E[i,] = E[i – 1,] + delta.SL[i,] – delta.LI[i,]
I[i,] = I[i – 1,] + delta.LI[i,] – delta.IR[i,]
R[i,] = R[i – 1,] + delta.IR[i,]
All that this proves is that the social distancing in Stockholm county (around 30-40%, not negligible at all; see https://www.gstatic.com/covid19/mobility/2020-05-16_SE_Mobility_Report_en.pdf ) has reduced R to 1.2 (which corresponds to HIT=17%)
If the population inhomogeneity theory was valid, it would have been observed in Lombardy and New York, where the spread happened before they had time to take measures.
About 20% of New Yorkers tested positive for antibodies to SARS-Cov-2 in the week leading up to 23 April: https://www.nytimes.com/2020/04/23/nyregion/coronavirus-antibodies-test-ny.html. That corresponds to cases of disease up to around 7 April. The peak of daily new cases was around the start of April, judging from the trailing weekly numbers (https://www.nytimes.com/2020/05/05/us/coronavirus-deaths-cases-united-states.html).
So it looks as if the HIT for NYC under lockdown was probably a little lower than 20%. Of course, it would be higher with Swedish policies, but maybe not that much higher.
In any event, I would expect the HIT to be considerably higher in NYC than in Stockholm, because it has a much higher propulation density, New Yorkers are probably naturally less socially distanced than Stockholm residents, and quite possibly on average they have higher susceptibility to infection (due, e.g., to higher obesity levels).
Have you thought about the role seasonality plays here? Norway and Denmark both released most of their lockdown measures, but cases continue to drop. I don’t think it’s plausible that they are anywhere near the HIT (I have my doubts on Swedenas well). I think it’s more plausible that the (enormous) change in daylight hours Scandinavia experiences in spring is responsible for the drop in cases across all countries.
Yes, I expect seasonality is a factor, but it’s difficult to quantify.
I didn’t suggest that Sweden as a whole had reached the HIT, just Stockholm County.
The point is that cases are also dropping in Oslo and Copenhagen, despite the fact that schools are running again, and businesses are open. I guess I’d be more convinced if your theory could explain why cases are dropping all over Scandinavia, rather than focusing on only one datapoint where we may have possibly reached HIT (or not).
Seen this Nic?
https://www.youtube.com/watch?v=dUOFeVIrOPg
Yes, I’m aware of that, thanks.
Hi Nick, happenstance put me on the website for judithcurry.com, which linked here.
I was struck by the 17% number from Stockholm County in Sweden.
Can I assume you are familiar with the ‘Diamond Princess cruise ship’. The link and quote below are there just in case you are not.
There are more data points in case you are are not. I also I build robot and am currently watching the Southwestern border from El Paso, Tx
All the Best
Jesse
—-
COVID-19 outbreak on the Diamond Princess cruise ship: estimating the epidemic potential and effectiveness of public health countermeasures
https://academic.oup.com/jtm/advance-article/doi/10.1093/jtm/taaa030/5766334
28 February 2020
Background
Cruise ships carry a large number of people in confined spaces with relative homogeneous mixing. On 3 February, 2020, an outbreak of COVID-19 on cruise ship Diamond Princess was reported with 10 initial cases, following an index case on board around 21-25th January. By 4th February, public health measures such as removal and isolation of ill passengers and quarantine of non-ill passengers were implemented. By 20th February, 619 of 3,700 passengers and crew (17%) were tested positive.
Yes, I’m familiar with the Diamond Princess data, thank you. I have an article based on its use, here.
Hi Nick,
There is a misunderstanding of the Swedish FHM presentation of data that leads you to think that there was a drop in cases after 11/4.
“Yet recorded new cases had stopped increasing by 11 April (Figure 1), as had net hospital admissions,[6] and both measures have fallen significantly since. That pattern indicates that the HIT had been reached by 11 April, at which point only 17% of the population appear to have been infected.”
FHM gets a bunch of reports per day, sort these by date and add number of infected to each day’s count. There is large lag, 1-2 weeks before the values stabilise. So, if you looked at the Stockholm’s incidence on the May 5 or so, you would see a number that will increase in subsequent days.
In your graph the value for may 5th is round 120, while it should be 173. Please have a look at the c19.se, pick Stockholm and there is a long table with daily values, one can substrata the previous day and get an incremental count. This site cuts off day the CET 0h, while FHM ar 11:30 am, so there could be some differences.
FHM site can also give you Stockholm’s value but it’s not easy to figure it out. But one should be able to download the raw data, pls let me know if I can assist you further.
Thank you for your comment. I am aware that some cases are reported late in Sweden, so the figures change – although usually by not very much after a few days. The delay in reporting deaths seems to be more of an issue.
Using the latest FHM daily case data for Stockholm region, and taking a 7-day average to iron out fluctuations and day of week distortions, the peak in cases was reached on 21 April. However, from the week ending 10 April (week 15) on, testing was increasingly being extended to healthcare workers, so the increase in cases does not reflect a greater number of infections. See Figure 1B in the FHM week 20 report, published on 25 May. This shows non-healthcare personnel cases (for which the test criteria remained the same) peaking in week to 10 April.
Thanks for answering, well, I’m looking at the weekly report week 23, last that had a split between health and non health workers, and week 15 and 16 looks similar in number of tests, mild/sever and non-heath worker/others.
The sharp drop in your diagram for the 5/5 is an artefact of reporting delays.
FHM publishes also Rt estimate, removing the health workers and primary care detected cases. The Rt stabilises round 1 at April 10, so it matches your HIT date.
Sweden test little (12% positive since week 20, even if testing increased from 40k to 60k, so incidence increases.
Somewhat I have problems with excluding health personnel, as they were up to 50% of all positive, and are an important infection vector, for various other reasons (no PPE, log held persuasion that no symptoms or no fever , no shedding and other nonsense).
It would be good to have an global Rt estimate, as unreliable as the rest of Swedish data.
There is little in it between weeks 14, 15 and 16 for severe, non-healthcare worker, cases – for which I believe the test criteria remained the same.
You say “Sweden test little (12% positive since week 20, even if testing increased from 40k to 60k, so incidence increases.” That doesn’t follow. If the criterion for testing (and test availability) was widened to include more milder, non-hospitalised cases, as it was, then the number of positive test results will increase even if incidence is unchanged, as previously unrecognised infections are increasingly included in the number of cases.
I think that much of the increase in test numbers from weeks 15 to 20 reflects increased testing of healthcare workers. The number of positive tests (cases) for healthcare workers increased by a factor of 2.4 between weeks 15 and 20, by about 1230, from 880 to 2110, but those for severe (hospitalised) cases dropped by ~40%. The total number of tests increased by 13123, with the overall number that were positive barely changed. Sippose one assumes that the proportion testing positive didn’t drop for severe cases (as the criteria for testing in such cases remained the same), and that in week 15 such cases accounted for 80% of 19,880 total tests (15,904), then tests for healthcare workers and in primary care increased by 17,099, or a factor of 5.3x, between weeks 15 and 20. Pro rating by positive test numbers in week 20, about 85% of this increase, some 14,550, relates to healthcare workers. That implies that, per the period as a whole, about 8.5% of healthcare workers tested during weeks 16 and 20 were infected. But, comparing the factor of 2.4x increase in positive tests results for them with my (admitedly imprecise) estimate of a factor of 5.3x rise in their testing, it seems fairly clear that their rate of infection was declining during that period.
IMHO there is a problem with the “herd immunity” concept as suggested by these models, a situation where the virus is extinguished with the models final R & S populations living happily forever.
Does ‘herd immunity’ exist at all in the context of the covid pandemic (serious pathogen)?
“Herd immunity” is the conclusion of a mathematical modelling with SIR and
derivate models. Its existence is based on a subtle mathematical
artefact of the model, the equal distribution of Susceptible and
Resistant (immunized) populations. Before anybody thinks that “herd
immunity” is a possibility in real world, this assumption should be
tested. The study (1) shows clearly that immunity is stratified in a
real population, both geographically and by age. So, the equal
distribution of R & S is not present in reality. One should add that
big parts of the society will be either protected (with PPE, like all
essential services in the society) or self isolated. The “herd
immunity”, in the case of an epidemic with a pathogen having potential
fatal outcome, is not achievable because its essential mechanism, the
randomisation of immunised (R) within a society is not happening. The
elements on the S compartment in the SIR type models are “unconscious”
mathematical objects modelling humans, unaware of the epidemic and not
taking any protective or evasive actions, this subtle mathematical
assumption is obviously not met when modelling serious infections.
For these reasons “herd immunity” in real world is a mathematical illusion,
and all policies based on it , like Sweden’s, are a tragic mistake.
(1)”Herd immunity is not a realistic exit strategy during a COVID-19 outbreak”
DOI:10.21203/rs.3.rs-25862/v1
https://www.researchsquare.com/article/rs-25862/v1
The study you cite makes the usual invalid claim that the natural herd immunity level is 50-70%, which is nonsense. It is bound to be lower than than the classic herd immunity level that applies where infection is randomised, as it is with vaccination. My article Why herd immunity to COVID-19 is reached much earlier than thought explains why, and gives examples of what it would be on various assumptions.
Agree, they have just repeated after some other studies, anyway, their findings are really about stratification of the Resistant, and at lower levels, they correspond to your findings.
Excellent paper. I have analyzed the same phenomenon using a large scale agent model with many knobs for variability in behavior, health, age, mobility and susceptibility. The “herd immunity” threshold varies with connectivity and demographics … but we have enough data to match exactly where we are and play out the scenarios going forward. Depending on the boundary conditions, the virus dies off infecting far fewer people than previously thought.
Here is my analysis on this topic completed back in May after I read the Gomes paper.
https://covidplanningtools.com/are-we-closer-to-herd-immunity-than-the-experts-say/
68% of people have SARS-COV-2 antibodies in densely populated Queens, New York.
https://www.nytimes.com/2020/07/09/nyregion/nyc-coronavirus-antibodies.html
In densely populated areas one would expect the reproduction number to be much higher than for the population as a whole, and there may be demographic differences that increase the susceptibility of the population to infection and/or reduce the dispersion of social connectivity relative to that of the entire population. Moreover, when an epidemic progesses unimpeded the final proportion of people infected will be well above the herd immunity threshold. So it is not terribly surprising that such a high percentage of the Queens population became infected and have developed antibodies to COVID-19.
Gets worse than that. Many who get infected do not have antibodies after a number of weeks, at least not detectable. So it’s likely much higher than 68%. Secondly, many of them who are getting detected with antibodies were part of one of the most severe lockdowns in the western world, and you just can’t deny that number would be higher otherwise, substantially higher.
Sweden and other countries may fare better having fewer densely populated areas, less travel between them, etc. But it’s not a scenario that applies to most of the world.
I don’t agree. For a start, prevalence in Queens, NYC, is most likely substantially lower than 68%. That figure came from a far from random sample: the tests were taken at an urgent care center! The article quotes Prof. Denis Nash, an epidemiology professor at the CUNY School of Public Health, as follows:
“For sure, the persons who are seeking antibody testing probably have a higher likelihood of being positive than the general population,” said Professor Nash. “If you went out in Corona and tested a representative sample, it wouldn’t be 68 percent.”
Moreover, one would expect individual neightbourhoods of a city to have less variability in susceptibility and social-connectivity related infectivity than the city as a whole, or even more so to that in the state containing the city. The smaller the sub-unit, the lower the expected variability within it.
I suspect that most of the people in NYC who had COVID-19 antibodies were infected prior to lockdown or before it became fully effective. In the UK, the chief medical officer has recently said that the epidemic was probably already past its peak (implying herd immunity had been achieved) prior to lockdown.
The NY Times article cites a more comprehensive survey on antibody rates conducted by New York State. It says “That survey suggested that roughly 21.6 percent of New York City residents had antibodies.” The study itself (https://doi.org/10.1101/2020.05.25.20113050) appears to show 20.2% cumulative incidence of COVID-19, or 22.7% when adjusted for the test sensitivity and for not all infected people generating detectable antibodies.
Lived-population density in Sweden (local population-density weighted by population) isn’t that low. And Stockholm is a fairly normal, and very internationally connected, large northern European city.